Optical Aberrations
Optical aberrations are the result of the less than perfect optical qualities of a telescope which can degrade an image. These include:
- piston
- tilt
- spherical aberration
- coma
- curvature of field
- astigmatism
- defocus
- distortion
- chromatic aberration
The optical aberrations of spherical aberration, coma, astigmatism, and chromatic aberration are well known to astronomers because they can affect most amateur astronomical equipment to some extent. Modern, optically well-corrected telescopes are designed to minimize or eliminate most of these aberrations.
Each of these optical aberrations has a distinct and quantifiable effect on image quality. Moreover, given a particular telescope and camera setup, the only optical aberration which is subject to immediate control by an astronomer is the defocus.
Defocus refers to the optical aberration resulting from less than perfect focus. In the case of a typical reflecting, refracting, or compound telescope, defocus tends to spread a star image in a circular fashion.
Nijboer-Zernike Theory
Nijboer-Zernike theory is a theory of diffraction in the presence of small optical aberrations, including all those listed above. Nijboer-Zernike theory was originally developed by Frits Zernike (Nobel Prize in Physics, 1953) and his doctoral student Bernard Nijboer, culminating in Nijboer's doctoral thesis in 1942. The original theory assumed the optics were in-focus. The theory has been advanced by later research as the Extended Nijboer-Zernike theory to include defocus. The Extended Nijboer-Zernike theory provides an analytic framework for the effects of the most common aberrations affecting astronomical images, including the effects of less than perfect focus.
In the Extended Nijboer-Zernike analytic framework, the interference pattern is described by the electromagnetic disturbance function:
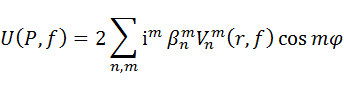
The original Nijboer-Zernike theory assumed in-focus, so its disturbance function U(P) omitted any reference to f, the defocus. The original Nijboer-Zernike disturbance U(P) is similar in form to the above except that the V(r, f) are replaced by Bessel functions of the first kind. In fact, the V(r, f) of the Extended Nijboer-Zernike equation are each a power series expansion involving the Bessel functions of the first kind. Anyone who has researched the technicalities of an Airy disk will recognize the Bessel function of the first kind of order one, usually denoted J1(x), which describes the Airy disk bull's-eye pattern.
The Extended Nijboer-Zernike equation describes the electromagnetic disturbance U at a point (or pixel) P on the camera sensor in the presence of defocus f. The disturbance U is an analytic quantity and is a complex number involving i, the so-called imaginary square-root of -1. The intensity of light at the point (or pixel) P on the camera sensor in the presence of defocus f is given by:
GoldFocus uses Extended Nijboer-Zernike theory for optical aberrations and defocus and Fresnel-Kirchhoff diffraction theory in the design of the GoldFocus Mask and Analysis Software.