Diffraction Theory

Light passing through an aperture causes interference patterns in the disturbed light waves. Most telescopes have a circular or an annular aperture. An annular aperture has a circular outer boundary with a circular central obstruction, such as the secondary mirror of a Newtonian reflector or a Cassegrain catadioptric. The diffraction pattern of a circular aperture disburses the light from a point source of light, such as a star, into a bull's-eye shaped image which is known as an Airy disk.
The Airy disk to the right is a simulated image of a point source of monochromatic (single-wavelength) light in the absence of blurring caused by astronomical seeing or any other effects. A gamma stretch has been applied to emphasize the otherwise very faint outer rings.
The net effect of diffraction through a circular or an annular aperture is to spread a point source of light, such as a star, into a larger circular shape.

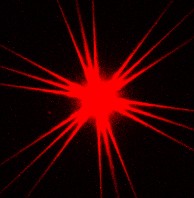
Another form of diffraction familiar to astronomers is caused by the spider vanes of a Newtonian reflector and their effects are commonly called Newtonian spikes. The Newtonian telescope image to the right is for visible light so includes a wide range of wavelengths.
It is natural to think of the spider vanes of a Newtonian reflector as being obstructions in the otherwise annular aperture. An equivalent interpretation is that the 4 spider vanes cut the annular aperture into 4 separate quadrant shaped apertures. For the purposes of analysis it is beneficial to adopt the interpretation of the spider vanes as creating a 4-part aperture where the interference patterns are caused by those four apertures.
Fresnel-Kirchhoff Theory
In an analytic framework with any arbitrary aperture - Newtonian spider vanes, annular, unobstructed circular, or any kind of purpose-built aperture diffraction mask - the interference pattern is more generally described by the electromagnetic disturbance function:
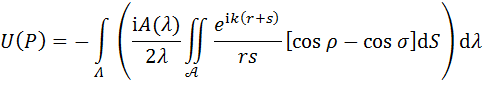
This equation is known as the Fresnel-Kirchhoff equation and is usually presented for only a single wavelength of light. The Fresnel-Kirchhoff equation above has been generalized to integrate all wavelengths to which the CCD camera sensor is sensitive or which pass any imaging filters being used.
The Fresnel-Kirchhoff equation describes the electromagnetic disturbance U at a point (or pixel) P on the camera sensor. The disturbance U is an analytic quantity and is a complex number involving i, the so-called imaginary square-root of -1. The intensity of light at the point (or pixel) P on the camera sensor is given by:
Max Born, the winner of the Nobel Prize in Physics, 1954, once wrote:
"Diffraction problems are amongst the most difficult ones encountered in optics." -- Max Born and Emil Wolf, Principles of Optics
The Fresnel-Kirchhoff equation is complicated. Max Born confirms it. The difficulty arises in integrating the integrands over the complicated apertures of useful aperture masks and integrating over the pertinent wavelengths. In only a very few special cases does the evaluation of the Fresnel-Kirchhoff equation over a specific aperture yield a simple solution and then only for a single wavelength of light, not simultaneously all wavelengths sensed by a camera.
GoldFocus uses Fresnel-Kirchhoff diffraction theory and Nijboer-Zernike theory in the design of the GoldFocus Mask and Analysis Software.